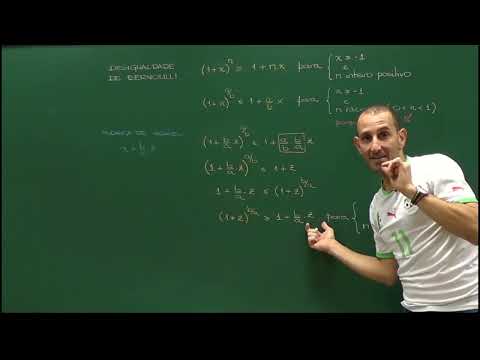Videoaula

Prova-se duas desigualdades: Problema 1: x + 1/x é maior ou igual a 2, para todo x positivo, com igualdade se e somente se x = 1. Problema 2: a/b + b/a é maior ou igual a 2, para quaisquer a, b positivos. Aproveita-se para destacar uma desigualdade que denominaremos Desigualdade Básica, que será a peça fundamental em muitas das desigualdades que veremos em aulas seguintes.

Resolve-se o seguinte problema: Problema 3: (a + b)(1/a + 1/b) é maior ou igual a 4, para quaisquer a, b positivos. Para tal, enfatizamos o uso da desigualdade básica e também a ideia de se provar uma desigualdade realizando um raciocínio de trás para frente.

Resolve-se de duas maneiras diferentes o seguinte problema: Problema 4: 1/a² + 1/b² é maior ou igual a 2/(ab), para quaisquer a, b não nulos. A primeira maneira consiste em fazer o raciocínio de trás para frente e obter a desigualdade básica. A segunda ensina que podemos substituir valores em uma desigualdade que sabemos ser verdadeira para deduzir novas desigualdades.

Resolve-se o Problema 5, um problema de comparação de áreas. Prova-se que ele é equivalente a mostrar que a² + b² + c² é maior ou igual a ab + ac + bc, e a resolução é uma aplicação da desigualdade básica. Aproveita-se para se destacar uma visualização geométrica do produto notável (a + b + c)² = a² + b² + c² + 2 (ab + ac + bc).

Resolve-se o Problema 6, uma generalização do Problema 3. Problema 6: (a_1 + ... + a_n) ( 1/a_1 + ... + 1/a_n ) é maior ou igual a n², para quaisquer a_1, ... , a_n positivos. A demonstração fornecida consiste em expandir a multiplicação e utilizar várias vezes a desigualdade provada no Problema 2.

Define-se as médias aritmética, MA e geométrica, MG. Prova-se a desigualdade das médias aritmética e geométrica: MA é maior ou igual a MG. Primeiro é feita a demonstração no caso em que temos apenas dois números e depois, através de um argumento por indução, prova-se o resultado que vale para qualquer quantidade de números.

Damos uma nova demonstração para o Problema 6, utilizando a recém-provada desigualdade MA-MG. Aproveitamos para introduzir uma nova média, a média harmônica.

A fim de contextualizar melhor a desigualdade das médias e deixar os ingredientes presentes nela mais naturais, apresentamos algumas situações em que a média geométrica aparece naturalmente.

Prosseguindo com nossa apresentação das diferentes médias, exibimos uma situação em que apesar de aparentemente precisarmos utilizar a média aritmética, na verdade, o que precisamos é da média harmônica.

Damos uma interpretação para a desigualdade das médias (para dois números apenas) através de uma construção geométrica. Na construção, dados dois números positivos nós construímos segmentos cujos comprimentos representam as médias aritmética, geométrica e harmônica. Tais segmentos podem ser comparados, evidenciando que MA é maior ou igual a MG, que é maior ou igual a MH.

Fornecemos uma demonstração de uma versão mais simples da desigualdade de Bernoulli, fazendo o desenvolvimento de (1 + x)^n através do Binômio de Newton, quando x é não negativo. Aproveitamos também para fazer uma analogia entre esta desigualdade e as taxas de juros simples e compostas.

Fazemos uma demonstração da desigualdade de Bernoulli por indução, que permite estender a desigualdade para x maior ou igual a -1. Depois, reinterpretamos a analogia com juros simples e compostos, para valores de taxa x compreendidos entre -1 e 0.

Usando a desigualdade MA-MG, mostramos uma versão da desigualdade de Bernoulli que vale para n número racional entre 0 e 1.

Analisamos a generalização da desigualdade de Bernoulli para n número racional maior que 1.

Aula 15 – Desigualdade de Cauchy-Schwarz

Começamos a usar as desigualdades que apresentamos para estudar alguns problemas de otimização. Nesta aula, estudamos algumas relações entre área de superfície, volume e diagonal de um paralelepípedo qualquer, usando a desigualdade de Cauchy-Schwarz.

Aplicamos a desigualdade das médias para resolver um problema em que queremos maximizar o volume de uma caixa sem tampa, considerando fixa sua área de superfície.

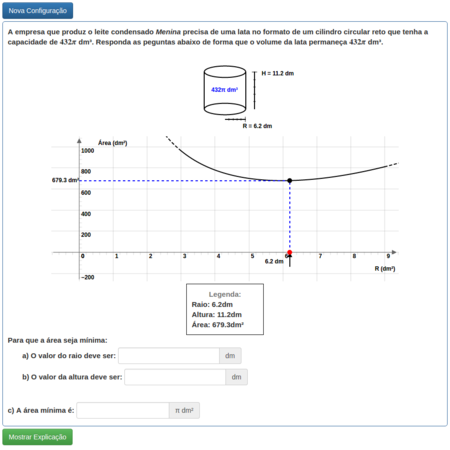
Aplicamos a desigualdade das médias para o problema de minimizar a área da superfície de um cilindro cujo volume é fixo; isto é, encontramos entre todos os cilindros que possuem o volume fixado, aquele que possui a menor área superficial.

Aplicamos a desigualdade das médias para encontrar o máximo da função f(x) = x^3 (1 – x) no intervalo [0,1], sem utilizar métodos mais avançados como a derivação.

Fazemos uma breve introdução aos vetores no plano, no espaço e em geral em um espaço de dimensão n. Definimos o que é o módulo de um vetor (seu comprimento) e o que é o produto interno (ou produto escalar) de dois vetores. Utilizando estas noções, reinterpretamos a desigualdade de Cauchy-Schwarz.

Após introduzir as ferramentas que precisamos no vídeo anterior, nós utilizamos a lei dos cossenos para obter uma fórmula alternativa para o produto interno de dois vetores. Esta nova representação fornece uma demonstração geométrica da desigualdade de Cauchy-Schwarz. Finalmente, utilizamos a desigualdade para demonstrar a desigualdade triangular no espaço n dimensional.