Videoaula
- Videoaula 13
- Caderno de Exercícios 1
- Aplicativo 2
- Teste
- Material Teórico 3
Outros Conteúdos da Aula
Aula 1 – Sequências definidas por recorrências
Definimos o que é uma sequência e apresentamos duas formas de descrever os termos de uma sequência. A primeira é a forma fechada, em que exibimos uma fórmula que apresenta o n-ésimo termo da sequência em função de n. A segunda é a forma recursiva, em que para obtermos o próximo termo da sequência nós utilizamos termos anteriores da sequência. Neste módulo, estudaremos as sequências obtidas desta segunda forma e também conhecidas como recorrências.
Aula 2 – Exemplos iniciais de recorrências
Damos alguns exemplos de sequências expressas por recorrências. Enfatizamos que para descrever uma sequência de forma recursiva é necessário, além de uma fórmula que relacione o próximo termo com os anteriores, exibir também termos iniciais da sequência para que ela fique bem determinada. Finalmente, reconhecemos progressões aritméticas e geométricas como exemplos de recorrências e ensinamos como descrevê-las desta forma.
Aula 03 - Recorrências que dependem de mais de um termo anterior
Nesta aula damos alguns exemplos de recorrências que utilizam em sua fórmula mais de um dos termos anteriores para descrever o próximo termo. Entre os exemplos, encontra-se a famosa sequência de Fibonacci e uma sequência cuja lei de formação é tomar a média aritmética dos números que já surgiram.
Aula 04 - Encontrando recorrências em polígonos convexos
Começamos a exemplificar como recorrências aparecem naturalmente em alguns tipos de problema. Nesta aula, encontramos duas fórmulas de recorrência. A primeira diz respeito ao valor da soma dos ângulos internos de um polígono convexo em função do seu número de vértices. A segunda trata sobre o número de diagonais de um polígono convexo.
Aula 05 - A Torre de Hanói
Ensinamos um jogo conhecido como a Torre de Hanói. Neste jogo, há três hastes e uma pilha com um certo número de discos empilhados em uma das hastes. O jogo consiste em transferir, utilizando a menor quantidade de movimentos possíveis, todos os discos da haste original para alguma outra haste, obedecendo determinadas regras. Utilizamos a ideia de recorrência para encontrar uma relação em que a quantidade mínima de movimentos para ganhar o jogo com n discos deve satisfazer.
Aula 06 - A Pizza de Steiner
Apresentamos o problema da Pizza de Steiner: Qual é o maior número de regiões em que se pode dividir o plano com n retas? A Pizza de Steiner fornece um novo exemplo de como podemos encontrar recorrências.
Aula 07 - Um problema com dominós
Nesta aula, encontramos uma equação de recorrência para a seguinte questão: De quantas formas diferentes podemos cobrir um tabuleiro 2xn usando peças de dominó? Surpreendentemente, a fórmula encontrada é uma recorrência bastante famosa.
Aula 08 - Recorrências lineares de primeira ordem
Após apresentarmos diversos problemas que podem ser entendidos utilizando recorrências, iniciamos um estudo mais aprofundado de tipos especiais de recorrência. Nesta aula, introduzimos as recorrências lineares de primeira ordem e mostramos dois exemplos de como encontrar uma fórmula fechada para recorrências deste tipo, isto é, de apresentar o n-ésimo termo como uma função apenas de n, sem fazer menção aos termos anteriores. Os exemplos apresentados são uma progressão aritmética e uma progressão geométrica que apareceram anteriormente na aula "Exemplos iniciais de recorrências".
Aula 09 - Recorrências e fórmulas fechadas - Parte 1
Utilizando as ideias da aula anterior, nós encontramos fórmulas fechadas para alguns dos problemas apresentados anteriormente: a soma dos ângulos internos de um polígono, o número de diagonais de um polígono e o problema da Pizza de Steiner. Isto é possível porque as recorrências de cada um destes problemas são de um tipo especial de recorrência de primeira ordem, em que o n-ésimo termo é dado pelo termo anterior mais uma função de n.
Aula 10 - Recorrências e fórmulas fechadas - Parte 2
Nesta aula, tratamos as recorrências lineares de primeira ordem em que o próximo termo da sequência é igual a uma constante vezes o termo anterior mais uma outra constante. A técnica que desenvolvemos nas últimas aulas ainda funciona, mas precisamos trabalhar um pouco mais para conseguir os cancelamentos necessários. Com isto, conseguimos encontrar uma fórmula fechada para o problema da Torre de Hanói, apresentado em uma aula anterior.
Aula 11 - Recorrências lineares homogêneas com coeficientes constantes
Desenvolvemos uma nova técnica para encontrar fórmulas fechadas para recorrências. Usando como base o formato geral de solução para uma recorrência linear com coeficientes constantes de primeira ordem, conseguimos encontrar a solução para uma recorrência linear de segunda ordem e coeficientes constantes.
Aula 12 - Fórmula fechada para a sequência de Fibonacci
Nesta aula, utilizamos o método que desenvolvemos na aula anterior para encontrar uma fórmula fechada para o n-ésimo termo da sequência de Fibonacci. Este método funciona, pois a recorrência que define a sequência de Fibonacci é linear e homogênea de segunda ordem, e com coeficientes constantes. A fórmula encontrada é surpreendente, pois envolve potências n-ésimas de números irracionais, mas ainda assim sempre fornece números inteiros. Esta fórmula também é interessante, pois nos leva a pensar sobre qual é a forma mais útil de se expressar uma sequência, já que a sequência de Fibonacci possui uma fórmula de recorrência muito simples e uma fórmula fechada complicada.
Aula 13 - Recorrências lineares de segunda ordem
Escrevemos, de maneira geral, qual é a fórmula fechada para uma recorrência linear de segunda ordem quando as raízes do polinômio característico são diferentes. Esta fórmula provém das técnicas que desenvolvemos nas últimas duas aulas. Além disso, fornecemos também a fórmula para quando o polinômio característico tiver uma raiz dupla.
Em Breve!
Em Breve!
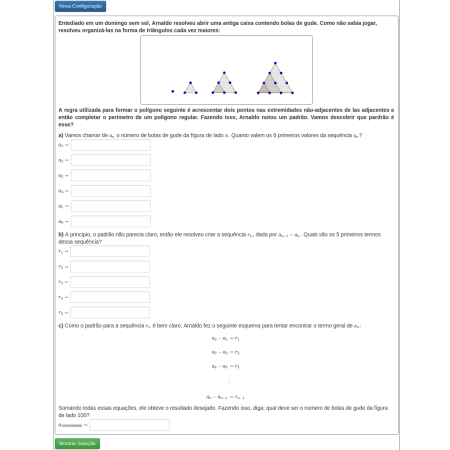
Números poligonais
Podemos usar recursões para encontrar padrões e prever termos de sequências. Vamos experimentar?
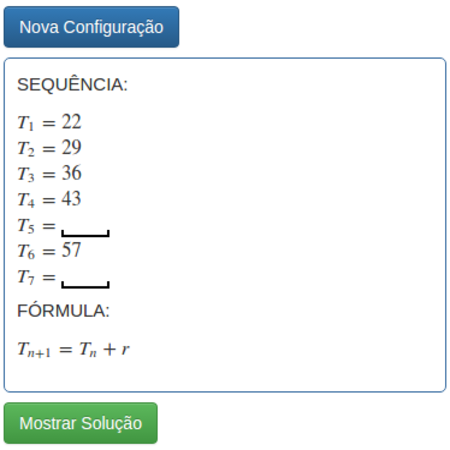
Descobrindo a sequência
Você é bom de notar padrões em sequências? Se não for tão simples, você pode recorrer à fórmula da sequência. Você gostaria de treinar?
Em Breve!
Recorrências - Parte 1
Começamos a estudar relações de recorrência, centrando nossa atenção na compreensão de sequências recorrentes e na tarefa de traduzir situações combinatórias em relações de recorrência
Recorrências - Parte 2
Continuamos a primeira parte da aula, desta vez estudando como resolver recorrências lineares de primeira ordem
Recorrências - Parte 3
Nessa última parte, aprendemos como resolver recorrências lineares de segunda ordem, homogêneas ou não