Videoaula
- Videoaula 12
- Exercícios Resolvidos 23
- Caderno de Exercícios 1
- Aplicativo 1
- Teste
- Material Teórico 3
Outros Conteúdos da Aula
Aula 1 – 1ª Demonstração: uma demonstração sem contas
Apresenta-se uma demonstração visual do Teorema de Pitágoras, baseada em uma comparação de áreas de duas figuras.
Aula 2 – 2ª Demonstração: calculando área de duas maneiras diferentes
Apresenta-se uma nova demonstração do Teorema de Pitágoras, através do cálculo da área de um trapézio de duas maneiras diferentes.
Aula 3 – Demonstração de Perigal - Parte 1
Esta é a primeira parte de uma demonstração do Teorema de Pitágoras dada por Perigal; tal demonstração é baseada em uma decomposição dos quadrados dos catetos em pedaços que, quando rearranjados, montam o quadrado da hipotenusa.
Aula 4 – Demonstração de Perigal - Parte 2
Esta é a segunda parte da demonstração do Teorema de Pitágoras dada por Perigal; tal demonstração é baseada em uma decomposição dos quadrados dos catetos em pedaços que, quando rearranjados, montam o quadrado da hipotenusa.
Aula 5 – Relações métricas simples
Utiliza-se o Teorema de Pitágoras para deduzir duas relações métricas simples e bastante utilizadas: o cálculo da diagonal do quadrado e da altura do triângulo equilátero em função de seus lados.
Aula 6 – Uma propriedade dos retângulos
Utilizamos o Teorema de Pitágoras para demonstrar a seguinte propriedade: seja ABCD um retângulo qualquer, com A e C vértices opostos. Fixe um ponto P no interior de ABCD. Então AP² + PC² = BP² + PD², isto é, as somas dos quadrados das distâncias de P a vértices opostos são iguais.
Aula 7 – A volta do Teorema de Pitágoras
Demonstramos um resultado geralmente pouco abordado: a volta do Teorema de Pitágoras. Em palavras, ela diz que se temos um triângulo ABC de lados BC = a, CA = b e AB = c com valores tais que a² = b² + c², então, tal triângulo é retângulo em A.
Aula 8 – Altura de um triângulo em função dos lados e a Fórmula de Herão
Nesta aula aplicamos o Teorema de Pitágoras para encontrar uma fórmula explícita que fornece o valor de uma altura do triângulo em função de seus lados. Uma aplicação direta deste resultado é obter uma fórmula para a área do triângulo em função de seus lados, resultado conhecido como Fórmula de Herão.
Aula 9 – Um exercício
Aplicamos o Teorema de Pitágoras juntamente com uma semelhança de triângulos para resolver um exercício em que queremos calcular a altura de um trapézio retângulo.
Aula 10 – Uma generalização do Teorema de Pitágoras e o Problema das Lúnulas de Hipócrates
Resolvemos um problema famoso, o problema das lúnulas de Hipócrates, de duas maneiras diferentes. Na primeira maneira, estudamos um caso particular e resolvemos fazendo as contas diretamente. Na segunda maneira, apresentamos uma bonita generalização do Teorema de Pitágoras que pode ser usada para dar uma solução direta ao caso geral deste problema.
Aula 11 – Lei dos Cossenos
A Lei dos Cossenos é uma generalização do Teorema de Pitágoras, pois pode ser aplicada para relacionar os 3 lados de um triângulo qualquer, não necessariamente retângulo, desde que saibamos algum dos ângulos dele. Nesta aula, provamos a Lei dos Cossenos utilizando o Teorema de Pitágoras.
Aula 12 – Exercício usando Teorema de Pitágoras e Lei dos Cossenos
Nesta aula resolvemos o seguinte exercício: Seja P um ponto interior de um triângulo equilátero ABC, tal que a distância de P para os vértices A, B e C é 3, 4 e 5 respectivamente. Encontre o lado do triângulo ABC. A resolução que damos para este problema utiliza a recíproca do Teorema de Pitágoras e a Lei dos Cossenos.
Em Breve!
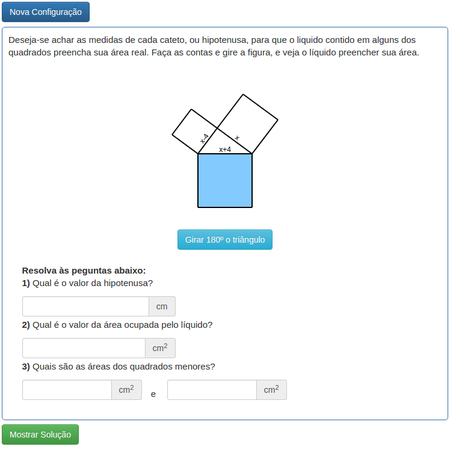
Teorema de Pitágoras e Aplicações
O Teorema de Pitagoras é bastante conhecido das nossas aulas de matemática e possui várias demonstrações interessantes. Resolva o problema do aplicativo e conheça mais uma demonstração.
Em Breve!
Algumas Demonstrações do Teorema de Pitágoras - Parte 1
Apresentamos quatro demonstrações distintas do Teorema de Pitágoras, com o intuito de enriquecer as ideias geométricas do leitor
Algumas Demonstrações do Teorema de Pitágoras - Parte 2
Após apresentarmos algumas demonstrações do Teorema de Pitágoras, voltamo-nos a aplicações interessantes do mesmo
Aplicações do Teorema de Pitágoras
Apresentamos, neste material teórico, mais aplicações interessantes do Teorema de Pitágoras