Aplicativo
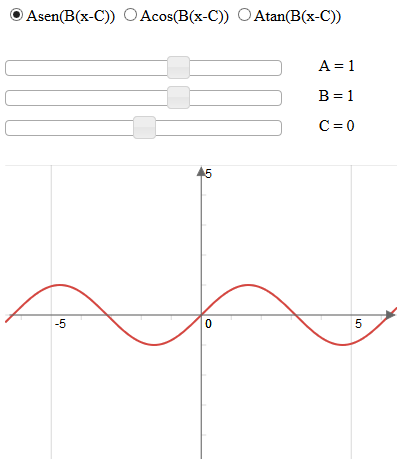
Grafico de Funções
As funções trigonométricas são funções angulares, importantes no estudo dos triângulos e na modelagem de fenômenos periódicos. Podem ser definidas de diversas formas, como a razão de lados em um triângulo retângulo; a razão entre projeções em um círculo unitário ou, até mesmo, como uma série infinita de potências.
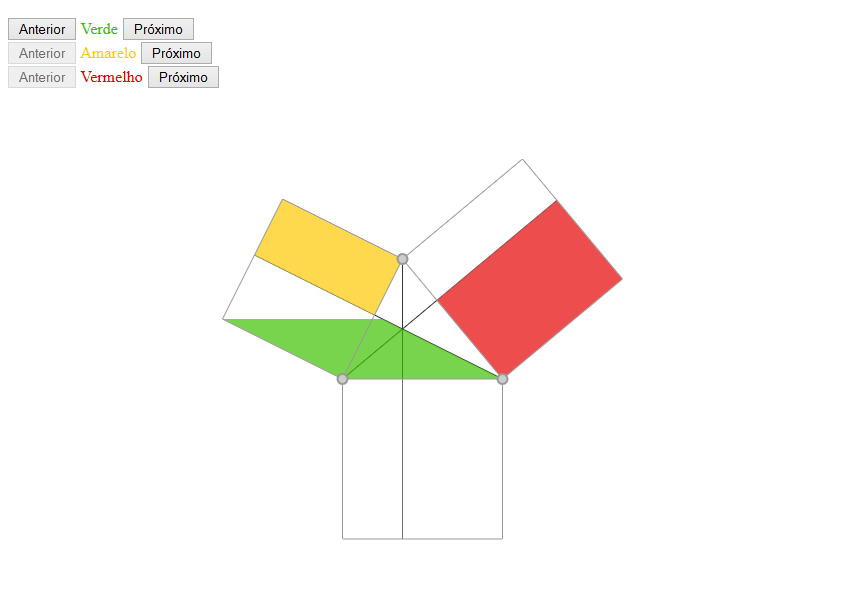
Lei dos Cossenos
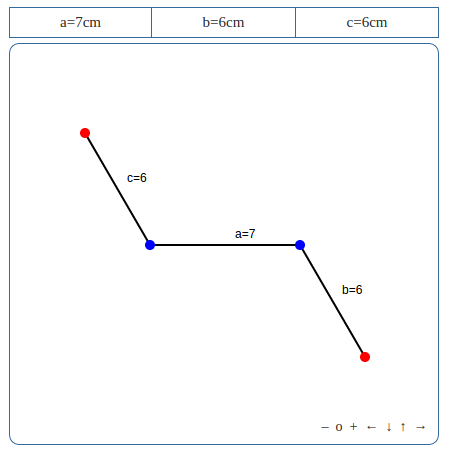
Esta aplicação é uma ajuda gráfica para a demonstração da lei dos cossenos. Esta lei é uma extensão do teorema de Pitágoras. O resultado assegura que em um triângulo cujos lados são a, b e c, e ângulos opostos aos lados A, B e C respectivamente são válidas as seguintes igualdades: [tex]\begin{eqnarray*} a^{2}=b^{2}+c^{2}-2bc\cos(\hat{A})\\ b^{2}=a^{2}+c^{2}-2ac\cos(\hat{B})\\ c^{2}=a^{2}+b^{2}-2ab\cos(\hat{C}) \end{eqnarray*}[/tex]. O resultado é verdadeiro para qualquer tipo de triângulo.
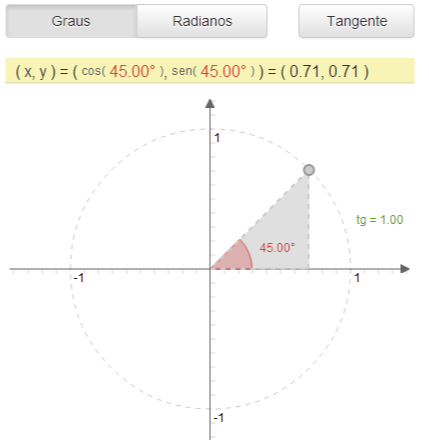
Relações Trigonométricas I
As funções trigonométricas podem ser definidas com base nas projeções em um círculo unitário. Nesta aplicação é explorada esta forma de defini-las.
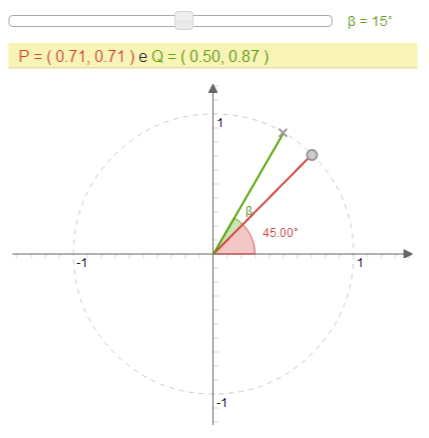
Relações Trigonométricas II
Esta aplicação é uma representação no círculo unitário do cosseno e seno da soma de dois ângulos. Selecione um ângulo [tex]\beta[/tex] na barra rolante.
Coleção de triângulos
O quanto você sabe de triângulos? Nesse interativo, exercitam-se as condições de existência de um triângulo com determinados lados, além da classificação do mesmo com respeito ao comprimento de seus lados e ângulos.